PROGNOZOWANIE SZEREGÓW RZADKICH
W praktyce często obserwujemy zjawiska, które nie zachowują ciągłości w czasie. Struktura danych nie jest regularna, istnieją wartości dominujące oraz duża zmienność. Przykładem mogą być dane sprzedażowe produktu, który nie był sprzedawany codziennie, ale co kilka dni lub rzadziej. W takim szeregu czasowym występuje wówczas wiele zer i to one są wartością dominującą, nie jest on spójny i standardowe metody prognozowania przestają być skuteczne.
W takiej sytuacji należy szukać innych metod - dostosowanych do szeregów rzadkich. W aplikacji firmy Prologistica używamy trzech algorytmów wyspecjalizowanych w prognozowaniu tego typu przypadków. Jest to występująca w literaturze metoda Crostona oraz dwa autorskie algorytmy: PDF oraz Schodkowy.
METODA CROSTONA
Algorytm ten jest znaną w literaturze metodą dekompozycji szeregu rzadkiego na dwa inne szeregi. Jeden z nich to szereg odstępów między kolejnymi sprzedażami, a drugi - wielkości tych sprzedaży. W ten sposób unikamy negatywnego wpływu dużej ilości zer.
W optymalizacji stanów magazynowych należy zwrócić uwagę na odpowiednie wykorzystanie takich prognoz. Przykładowo, jeśli prognozą następnej sprzedaży jest 300 sztuk, a prognozą czasu oczekiwania na sprzedaż jest 10 dni, to wówczas możemy uznać, że prognoza na każde kolejne 10 dni to wartość 30 sztuk (zamiast przyjmować na 9 dni same zera, a dziesiątego dnia 300 sztuk). Nie jest to w praktyce raczej możliwe, ale w teorii zapasów pozwala utrzymać część zapasu w magazynie i chroni przed spadkiem poziomu obsługi klienta.
METODA PDF
Algorytm ten jest najskuteczniejszy w przypadku danych, które nie charakteryzują się widoczną sezonowością ani występującym w nich trendem, innymi słowy wykorzystywany jest głównie wtedy, gdy wartości są w miarę ustabilizowane wokół pewnego poziomu. Główną ideą metody jest dopasowanie – na podstawie zaawansowanych testów, rozkładu prawdopodobieństwa do danych. Gdy żaden rozkład nie okaże się skuteczny, wówczas stosujemy techniki bootstrapowe.
METODA SCHODKOWA
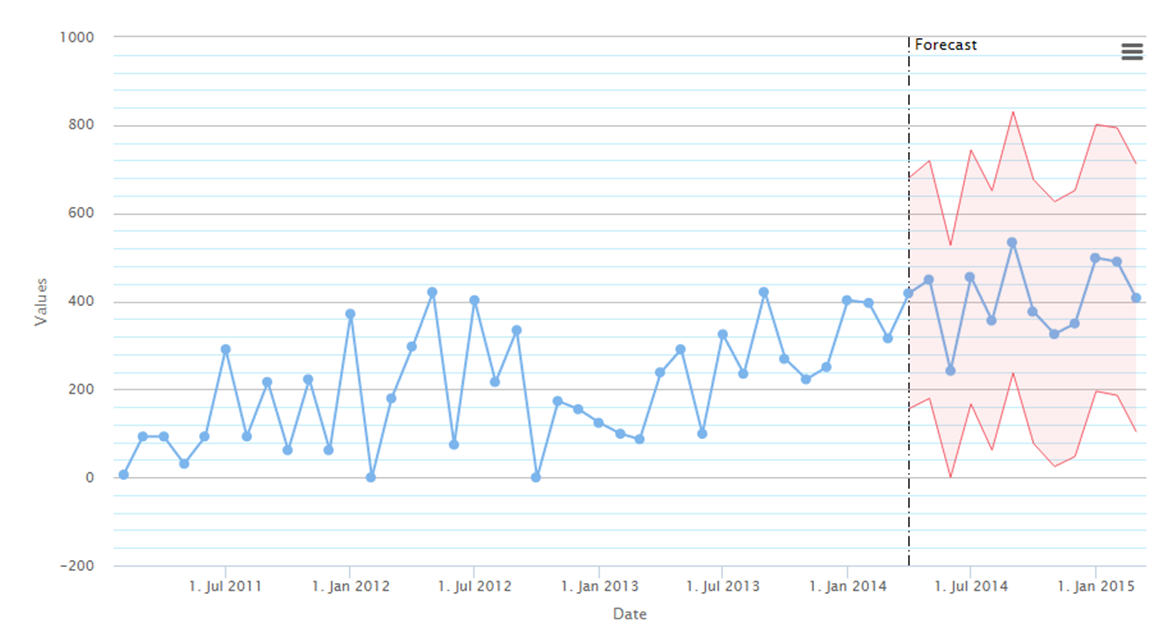
Ideą tego algorytmu jest agregacja danych i wykorzystanie faktu, że podczas grupowania danych, zmniejsza się rzadkość szeregu. Szereg rzadki przedstawiający dzienną sprzedaż zagregowany do miesięcy będzie znacznie bardziej ciągły, przez co możliwy do prognozowania klasycznymi metodami takimi jak ARIMA.
Poprzedni szereg wraz z prognozą po agregacji
Możemy dzięki temu uwzględniać sezonowość i występowanie tendencji rozwojowych w danych, których nie było widać w niższej agregacji.
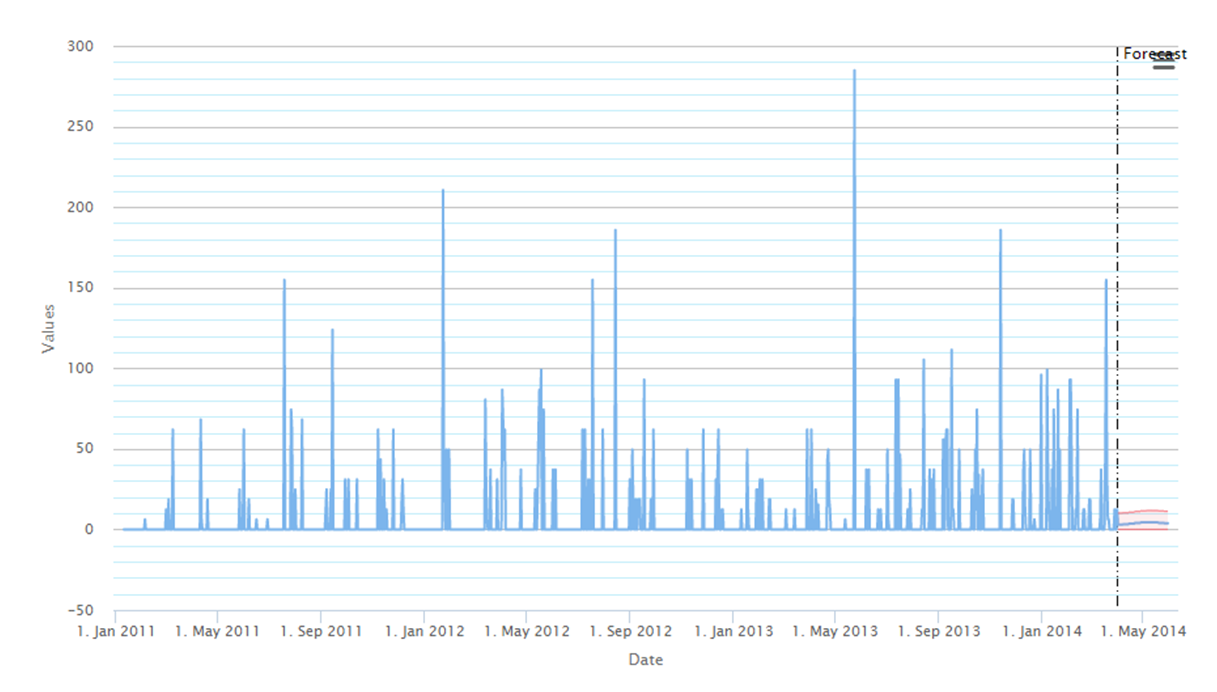
Ten sam szereg ponownie w agregacji dziennej wraz z uzgodnioną prognozą
Bardzo ważną kwestią jest odpowiednia interpretacja takich prognoz. W podejściu klasycznym dla szeregów ciągłych, celem było wygenerowanie prognoz, które jak najlepiej oddałyby wizualny charakter przyszłych wartości. W przypadku szeregów rzadkich nie jest to możliwe. Dlatego możliwą strategią takiego prognozowania są prognozy płaskie w danych okresach. Nie można dokładnie przewidzieć kiedy po wielu tygodniach braku sprzedaży, w końcu ona nastąpi i jakiej będzie wielkości. Można jednak przewidzieć sumę sprzedaży w danym okresie i rozłożyć ją w określony sposób na dni. Ma to szczególne znaczenie w procesie optymalizacji zapasów - potrzebujemy pewną małą ilość zapasów na każdy dzień (mimo, że sprzedaż nie występuje) ale w ten sposób, gdy w końcu nastąpi duża sprzedaż - będziemy na to przygotowani.