Prognozy przedziałowe

Większość osób odpowiedzialnych za prognozowania w przedsiębiorstwach zadowala się prognozami punktowymi. No bo właściwie, jak stworzyć przedział ufności dla średniej? Regresja w arkuszu kalkulacyjnym także nie wylicza przedziałów, trzeba by samemu szukać wzorów.

A czym w ogóle są przedziały? Prognoza punktowa to po prostu jedna wartość, przykładowo średni kurs franka do złotego we wrześniu 2011 wyniesie 3,73. Prognoza przedziałowa to wartości wśród których z określonym prawdopodobieństwem znajdzie się przyszła obserwacja, np. średni kurs franka do złotego we wrześniu 2011 z 95% prawdopodobieństwem znajdzie się pomiędzy: 3,62 a 3,97 (liczby przykładowe, nie ma co na nie grać :) ).

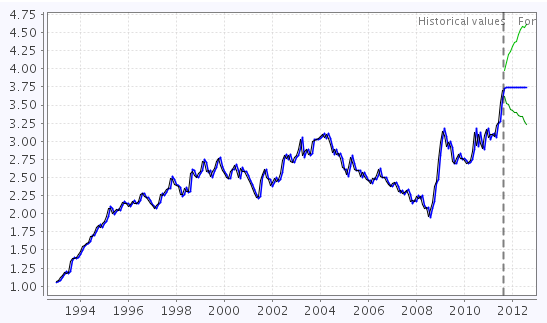
Co dają nam przedziały ufności dla prognoz?

Największą korzyścią z prognoz przedziałowych jest to, że analityk od razu widzi z jak dużą niepewnością wiąże się prognoza. Widząc na jednym wykresie prognozy punktowe i przedziałowe, po szerokości tych przedziałów od razu wiadomo jak dobry jest model i jak bardzo można polegać na prognozie. Taka graficzna reprezentacja jest bardziej intuicyjna niż jakikolwiek wskaźnik liczbowy. Co więcej, bazując na prognozach przedziałowych możemy przygotowywać plany optymistyczne i pesymistyczne. Poziomem ufności można też sterować, tak żeby przedział odpowiadał, np. za 80% a nie 95%, lub 99%.

Jak liczyć przedziały ufności?

Dla różnych metod prognozowania są różne wzory. Dla modeli regresji błędy prognoz ex-ante znajdują się na przekątnej macierzy:



X* ? to macierz przyszłych wartości zmiennych objaśniających, S_e to odchylenie standardowe reszt z modelu.

Przemnożenie tych wartości przez odpowiedni współczynnik (np. 1,96 dla rozkładu normalnego reszt i 95% przedziału ufności) i dodanie/odjęcie od wartości prognozy punktowej da nam przedział ufności dla prognoz.

Niektóre metody nie mają podanych wzorów na wariancję błędu prognozy (błąd ex-ante), ani, co za tym idzie, na przedziały ufności dla prognoz. Wzory te mogą być też bardzo skomplikowane. Tak jest np. z wygładzaniem wykładniczym. W przypadku tej grupy metod znacznie łatwiej przeprowadzić symulację i wykonać kilkaset/kilka tysięcy prognoz wykorzystując błędy z modelu. Na podstawie takiej symulacji tworzy się przedziały ufności korzystające z rzeczywistego rozkładu reszt (brak założenia o ich normalności). Trzeba tylko dysponować odpowiednim programem do przeprowadzenia takiej symulacji.

Podsumowując, przedziały ufności dla prognoz dają nam znacznie więcej informacji na temat prognozy. Pokazują nam z jakim poziomem niepewności się wiążą i pozwalają przygotować się na różne scenariusze. Ich interpretacja jest bardzo prosta, potrzeba jedynie odpowiedniego narzędzia do ich obliczania.