SARIMA / ARIMA X13
SARIMAModele (S)ARIMA należą do najczęściej stosowanych i najskuteczniejszych metod prognozowania szeregów czasowych. Potrafią one uwzględnić wiele różnych struktur niedających się zaobserwować podczas zwykłej wizualnej analizy. W szczególności możemy wykryć istniejące trendy oraz wahania sezonowe. Konstrukcja tej klasy modeli polega na stopniowym uogólnianiu prostych metod autoregresji i ruchomej średniej:
- Model autoregresji AR(p):
gdzie
to parametry modelu,
to zakłócenie (biały szum), a c to stała
- Model ruchomej średniej MA(q):
gdzie
to parametry modelu,
to zakłócenie (biały szum), a
średnia szeregu
- Model ARMA(p, q):
będący połączeniem dwóch poprzednich
- Model ARIMA(p, d, q): uogólnienie poprzedniego modelu w celu opisu zjawisk niestacjonarnych – po d – krotnym zróżnicowaniu otrzymujemy ponownie model ARMA(p, q). Celem różnicowania jest eliminacja trendu. Różnicowanie I rzędu polega na wyliczeniu szeregu różnic
, różnicowanie II rzędu na wyliczeniu
itd.
- Model SARIMA(p, d, q)(P, D, Q): model ARIMA, który uwzględnia składową sezonowości (P – rząd opóźnień sezonowych typu AR, Q – rząd opóźnień sezonowych typu MA, D – różnicowanie składowej sezonowej).
Kluczowym zadaniem jest wybór rzędu modelu, czyli liczb p, d, q, P, D, Q. Dobrym podejściem i stosowanym w firmie ProLogistica jest podział obserwacji na zbiór testowy i uczący, budowa wielu różnych modeli na zbiorze testowym i porównanie ich prognoz ze zbiorem uczącym. Model ze współczynnikami, generujący prognozy obarczone najmniejszym błędem jest preferowany. Następnym krokiem jest dołączenie pozostałych obserwacji i ponowna estymacja parametrów.
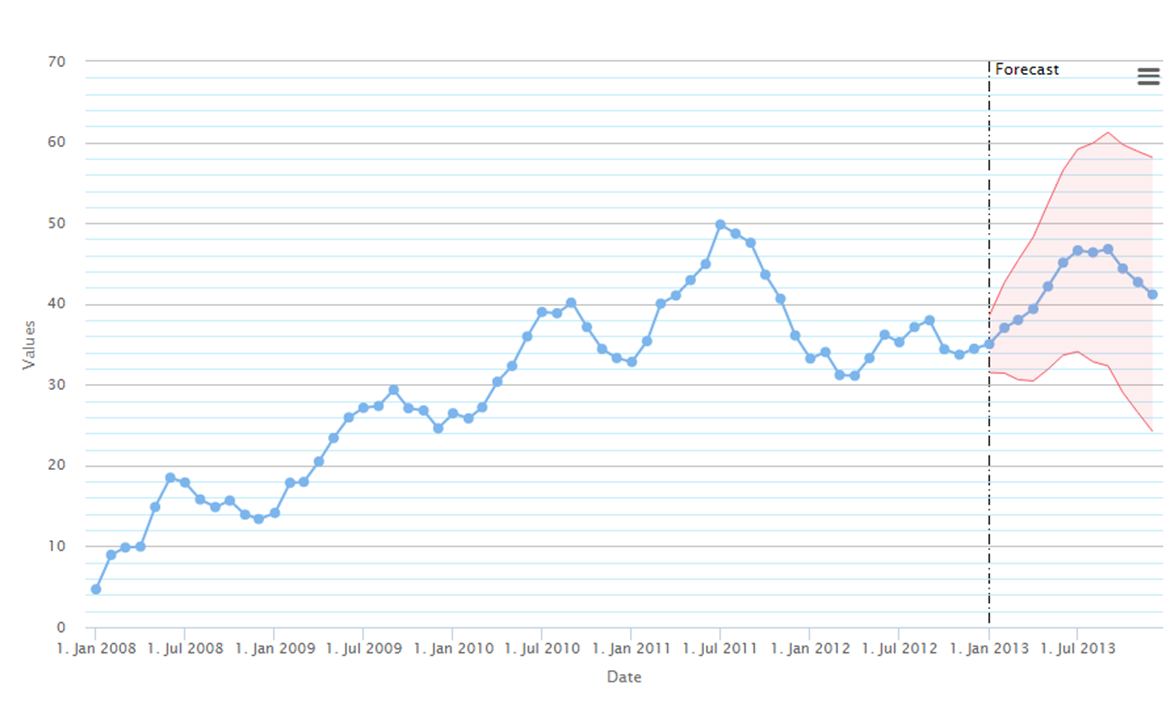
Szereg z trendem i sezonowością, model SARIMA (2, 1, 0)(1, 0, 1)
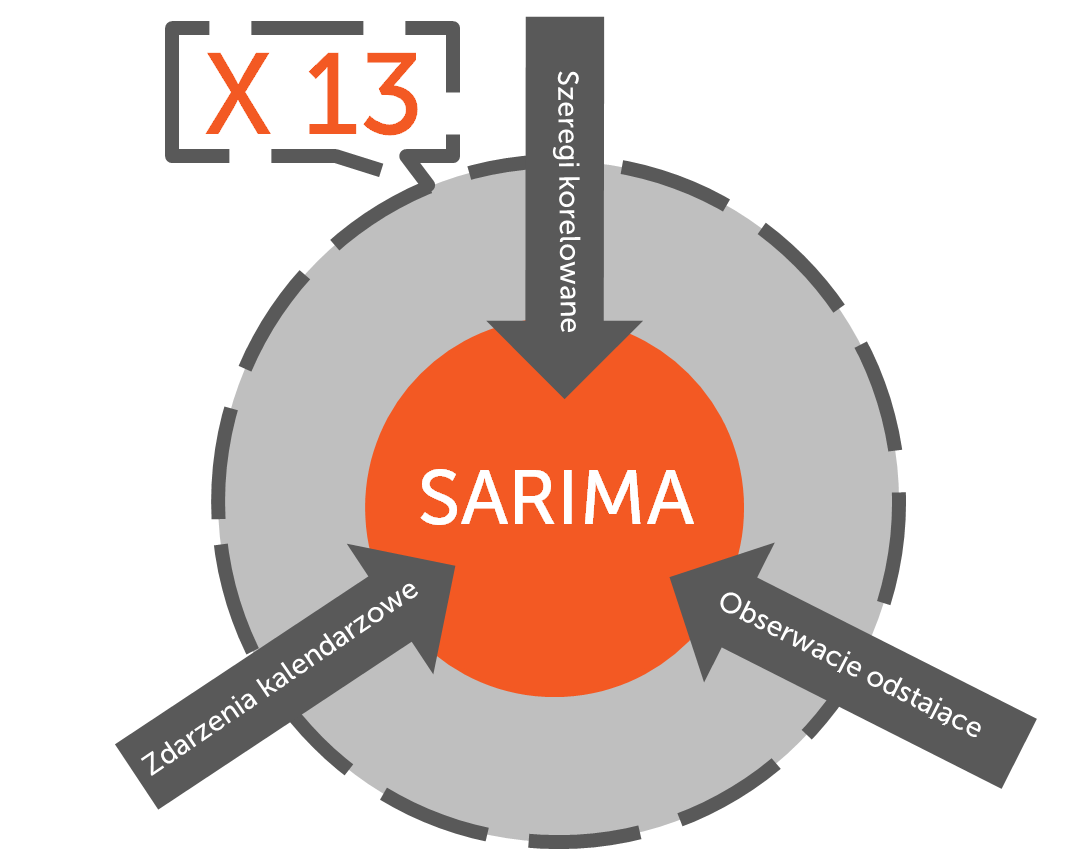
ARIMA X13
Ideą algorytmu jest połączenie modeli (S)ARIMA z modelem regresji liniowej. Własności modeli ARIMA z różnicowaniem sezonowym i zwykłym umożliwiają modelowanie trendu i sezonowości oraz ulepszają analizę składnika reszt, zaś model regresyjny pozwala dodatkowo na wprowadzanie zmiennych opisujących zdarzenia kalendarzowe, takie jak święta czy inne dni wolne od pracy, w których nie następuje sprzedaż.
Możemy też wprowadzać obserwacje odstające, czyli nietypowe, duże sprzedaże, które mogły być tylko jednorazowym zamówieniem i bez ich wykrycia prognozy byłby zbyt wysokie. Kolejną możliwością jest uzależnienie prognoz jednego czynnika od drugiego. Polega to na przewidywaniu przyszłych wartości przy pomocy innych, łatwiejszych do prognozowania danych np. przewidywania na temat sprzedaży produktu sezonowego przy użyciu przyszłych wartości temperatury. Taki pomocniczy szereg nazywamy szeregiem korelowanym.
Metodologia ta jest intensywnie rozwijana i wykorzystywana przez amerykański urząd statystyczny oraz liczne instytucje na świecie.
W naszej firmie wykorzystujemy testy sezonowości i stacjonarności, które pozwalają z góry ograniczyć ilość rozpatrywanych modeli i znaczenie przyspieszyć czas obliczeń. Posiadamy również specjalny algorytm przeszukiwania wybranych kombinacji parametrów, który pozwala wybrać adekwatny model w krótszym czasie niż zazwyczaj – bez konieczności sprawdzania wszystkich parametrów.